Состояние акселератора

2.1.1.1. Память акселератора

Ячейка памяти представляет собой набор двоичных переменных (далее битов), с возможными значениями 0 или 1. Число битов определяет разрядность ячейки. Набор из одной или более ячеек одинаковой разрядности образует область памяти. Набор из одной или более областей образует память. Память будем обозначать большой буквой S. Состояние ячейки памяти определяется набором конкретных значений всех ее битов. Состояние памяти определяется состоянием всех ячеек ее областей. Состояние памяти будем обозначать маленькой буквой s. Обозначим через N сумму разрядностей всех ячеек памяти S, тогда память может находиться в одном из 2N состояний. Множество состояний памяти будем обозначать {s}. Заметим, что это множество однозначно задается структурой памяти. Дескриптор структуры памяти

представляет собой следующий набор чисел: число областей O и набор из O пар (Wi, Si), задающих разрядность Wi ячеек области и их количество Si.

В нашей модели память системы состоит из памяти основного процессора SP, разделяемой памяти SS и локальных памятей акселераторов Sa:

, - число акселераторов

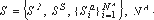
Рассмотрение памяти процессора не принципиально для данной статьи, так как акселератор имеет доступ только к разделяемой и своей локальной памяти. Пара из этих памятей формирует полную память акселератора:

SA={SS,Sa}

Множество возможных состояний памяти акселератора обозначим как {S}A={S}Sx{S}a. Каждая область в локальной и разделяемой памяти характе-ризуется скоростью доступа - числом, означающим, сколько тактов проходит после записи в ячейку этой области, прежде чем измененное значение может быть прочитано; до этого момента при чтении считывается старое значение.

Обычно в памяти акселератора можно выделить следующие области:

Набор из одной или более памятей данных
Набор из одного или более регистровых файлов
Одиночные регистры

2.1.1.2. Управляющее состояние

Акселератор имеет фиксированное количество управляющих слотов, совокупность которых обозначается pA. Каждый слот имеет номер, который далее будет отождествляться с соответствующим слотом.
Каждый слот Li представляет собой пару целочисленных переменных (полей): поле номера команды nf и поле состояния команды t. Множество значений поля команды {nf} конечно. Ноль всегда принадлежит {nf}. Существует взаимно однозначное соответствие между {nf}\0 и множеством дескрипторов команд, определение которого будет дано ниже. Поэтому мы будем отождествлять номер

и соответсвующий дескриптор f. Множество значений поля состояния команды есть натуральные числа (включая 0). Состояние слота с номером n обозначается ln=(nf,t) и определяется значениями полей этого слота. Множество возможных состояний слота {l}n={nf}xN. Слот в состоянии (0, 0) называется свободным, в ином случае активным. Управляющим состоянием p акселератора называется совокупность состояний всех его управляющих слотов. Множество управляющих состояний акселератора обозначим {p}A={l}NE, где Ns число слотов акселератора. Активные слоты соответствуют выполняющимся командам акселератора, число управляющих слотов задает максимальное количество параллельно выполняющихся команд. В состоянии активного слота значение поля номера команды задает выполняющуюся команду, а значение поля состояния команды соответствует количеству тактов, прошедших с начала выполнения этой команды.

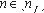
2.1.1.3. Состояние акселератора Состояние акселератора a задается парой из состояния памяти и управляющего состояния: a={s, p}. Множество состояний акселератора обозначим как {a}A={S}Ax{p}A.

Элементом состояния акселератора называется любая ячейка памяти акселератора или любой управляющий слот. Состоянием элемента называется соответственно состояние ячейки или слота. Параллельной композицией функций ?1,?2,...,?n (заданных на множестве состояний акселератора) назовем функцию ? = ?1?2...?n(также заданную на множестве состояний акселератора), получаемую следующим образом: пусть

множество всех элементов состояния акселератора, Ai - множество элементов, состояние a? которых было изменено функцией

.

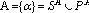
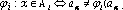
Если пересечение всех Ai,i=1..n не пустое множество, то значение функции ? не определено.В ином случае значение ? задается следующим образом:

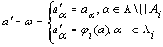, здесь a`? и a`? - новое и старое состояние элемента соответственно

Содержание раздела